Pointed space

In mathematics, a pointed space is a topological space X with a distinguished basepoint x₀ in X. Maps of pointed spaces (based maps) are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f(x₀) = y₀. This is usually denoted

f : (X, x₀) → (Y, y₀).

Pointed spaces are important in algebraic topology, particularly in homotopy theory, where many constructions, such as the fundamental group, depend on a choice of basepoint.

The pointed set concept is less important; it is anyway the case of a pointed discrete space.

Category of pointed spaces

The class of all pointed spaces forms a category Top_• with basepoint preserving continuous maps as morphisms. Another way to think about this category is as the comma category, ({•} ↓ Top) where {•} is any one point space and Top is the category of topological spaces. (This is also called a coslice category denoted {•}/Top.) Objects in this category are continuous maps {•} → X. Such morphisms can be thought of as picking out a basepoint in X. Morphisms in ({•} ↓ Top) are morphisms in Top for which the following diagram commutes:

It is easy to see that commutativity of the diagram is equivalent to the condition that f preserves basepoints.

As a pointed space {•} is a zero object in Top_• while it is only a terminal object in Top.

There is a forgetful functor Top_• → Top which "forgets" which point is the basepoint. This functor has a left adjoint which assigns to each topological space X the disjoint union of X and a one point space {•} whose single element is taken to be the basepoint.

Operations on pointed spaces

A subspace of a pointed space X is a topological subspace A ⊆ X which shares its basepoint with X so that the inclusion map is basepoint preserving.
One can form the quotient of a pointed space X under any equivalence relation. The basepoint of the quotient is the image of the basepoint in X under the quotient map.
One can form the product of two pointed spaces (X, x₀), (Y, y₀) as the topological product X × Y with (x₀, y₀) serving as the basepoint.
The coproduct in the category of pointed spaces is the wedge sum, which can be thought of as the one-point union of spaces.
The smash product of two pointed spaces is essentially the quotient of the direct product and the wedge sum. The smash product turns the category of pointed spaces into a symmetric monoidal category with the pointed 0-sphere as the unit object.
The reduced suspension ΣX of a pointed space X is (up to a homeomorphism) the smash product of X and the pointed circle S¹.
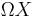The reduced suspension is a functor from the category of pointed spaces to itself. This functor is a left adjoint to the functor $\Omega$ taking a based space $X$ to its loop space $\Omega X$ .

References

Gamelin, Theodore W.; Greene, Robert Everist (1999) [1983]. Introduction to Topology (second ed.). Dover Publications. ISBN 0-486-40680-6.
Mac Lane, Saunders (September 1998). Categories for the Working Mathematician (second ed.). Springer. ISBN 0-387-98403-8.